[머신러닝] 선형 회귀

-

선형 회귀


선형 회귀(Linear Regression)


아래 마인드 맵에 나와있는 것 처럼 선형 회귀는 지도 학습의 대표적인 회귀 알고리즘이다.
(Machine Learning -> Unsupervised Learning -> Linear Regression)





선형 회귀는 특성과 타깃 사이의 관계를 가장 잘 나타내는 선형 방정식을 찾는다.
특성이 하나인 경우 어떤 직선을 학습하는 알고리즘이다. 



K-최근접 이웃 회귀의 문제점


선형 회귀에 대해 알아보기 전에 K-최근접 이웃 회귀의 문제점을 알아보자. 아래 예제를 복붙해서 한번 실행해 보길 바란다.
import numpy as np

height = np.array([10.0,11.0,12.0,13.0,14.0,15.0,16.0,17.0,18.0,19.0,
                   20.5,21.0,22.0,23.0,24.0,25.0,26.0,27.5,28.0,29.0,
                   30.0,31.0,32.0,33.0,34.0,35.0,36.0,37.0,37.5,38.0,
                   39.0,40.0,41.0,42.0,43.0,44.0,45.0,46.0,47.0,48.0,
                   49.0,50.0,51.3,52.0,53.0,54.0,55.0,56.0,57.0,58.0
                    ])

weight = np.array([100.0,101.9,102.0,103.0,104.0,105.0,106.0,107.0,108.0,109.0,
                   110.0,110.0,111.0,120.0,121.0,122.0,124.0,126.0,127.0,128.0,
                   130.0,135.0,137.0,138.0,140.0,150.0,151.0,155.0,160.0,162.0,
                   170.0,180.0,190.0,200.0,300.0,400.0,500.0,600.0,700.0,800.0,
                   850.0,850.0,860.5,870.7,880.0,890.0,900.0,920.0,930.0,950.0
                    ])


#훈련세트,테스트 세트 나누기. random_stata를 42로 하면 프로그램을 껐다켜도 훈련세트와 테스트 세트의 샘플이 유지된다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
    height, weight, random_state=42)

# 2차원으로 바꾸기
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)

#모델 훈련 시키기
from sklearn.neighbors import KNeighborsRegressor

knr = KNeighborsRegressor()
knr.fit(train_input, train_target)

#훈련 시키기
knr.fit(train_input, train_target)

#60 height 예측하고 출력하기
print(knr.predict([[70]]))
결과 : [904.14]

결과가 이상하지 않은가? height 특성에서 가장 높은 58.0 보다 더 높은 70을 예측했는데 예측 결과가 904.14로 weight 특성 중 가장 높은 950.0 보다 더 작게 나온다.


훈련세트와 예측 샘플을 산점도로 나타내는 예제를 실행 시켜 보자.
import matplotlib.pyplot as plt #그래프 그리는 패키지 import

plt.scatter(train_input, train_target, color='red')

#60, 904.14 예측 데이터 그리기
plt.scatter([70], [904.14], color='green', marker='*')

plt.xlabel('height')
plt.ylabel('weight')
plt.show()



산점도를 보니 확실히 예측 샘플이 height는 높은데 weight 상대적으로 낮다는 것을 확인 할 수 있다.




이유는 간단하다. K-최근접 이웃 뿐 아니라 K-최근접 이웃 회귀 알고리즘도 주변의 K개의 샘플들의 weight를 평균하기 때문에 예측 데이터의 weight가 낮게 나오는 거다. 그렇다면 아무리 height가 높더라도 weight는 더 이상 오를 수가 없다.



데이터 준비하기


회귀 알고리즘을 사용하기 전 데이터를 준비하자. K-최근접 이웃 알고리즘의 데이터와 동일하다.
import numpy as np

height = np.array([10.0,11.0,12.0,13.0,14.0,15.0,16.0,17.0,18.0,19.0,
                   20.5,21.0,22.0,23.0,24.0,25.0,26.0,27.5,28.0,29.0,
                   30.0,31.0,32.0,33.0,34.0,35.0,36.0,37.0,37.5,38.0,
                   39.0,40.0,41.0,42.0,43.0,44.0,45.0,46.0,47.0,48.0,
                   49.0,50.0,51.3,52.0,53.0,54.0,55.0,56.0,57.0,58.0
                    ])

weight = np.array([100.0,101.9,102.0,103.0,104.0,105.0,106.0,107.0,108.0,109.0,
                   110.0,110.0,111.0,120.0,121.0,122.0,124.0,126.0,127.0,128.0,
                   130.0,135.0,137.0,138.0,140.0,150.0,151.0,155.0,160.0,162.0,
                   170.0,180.0,190.0,200.0,300.0,400.0,500.0,600.0,700.0,800.0,
                   850.0,850.0,860.5,870.7,880.0,890.0,900.0,920.0,930.0,950.0
                    ])


#훈련세트,테스트 세트 나누기. random_stata를 42로 하면 프로그램을 껐다켜도 훈련세트와 테스트 세트의 샘플이 유지된다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
    height, weight, random_state=42)

# 2차원으로 바꾸기
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)


훈련 시키기


훈련 시켜보자. 
이때 LinearRegression 클래스를 import 해준다.
#모델 훈련 시키기
from sklearn.linear_model import LinearRegression

lr = LinearRegression()

#선형 회귀 모델 훈련
lr.fit(train_input, train_target)

#예측하고 출력하기
print(lr.predict([[60]]))
결과 : [1008.57662241]

오, 결과를 보니 확실히 weight 예측 값이 이전보다 높아졌다.



산점도 그리기


수치도 봤으니 산점도로 확인 해보자.
import matplotlib.pyplot as plt #그래프 그리는 패키지 import

plt.scatter(train_input, train_target, color='red')

#예측 데이터 그리기
plt.scatter([70], [1008.57662241], color='green', marker='*')

plt.xlabel('height')
plt.ylabel('weight')
plt.show()



확실히 K-최근접 이웃 회귀 알고리즘을 사용 했을 때와 다르게 선형 회귀는 height에 따라 weight가 상승한 것을 볼 수 있다.



선형 회귀가 학습한 직선


선형 회귀는 특성이 하나인 경우 어떤 직선을 학습하는 알고리즘이라고 했다. 예제 에서는 height 특성 하나만 보고 직선을 학습 했다. 그렇다면 어떻게 직선을 학습 한 걸까?



직선의 방정식


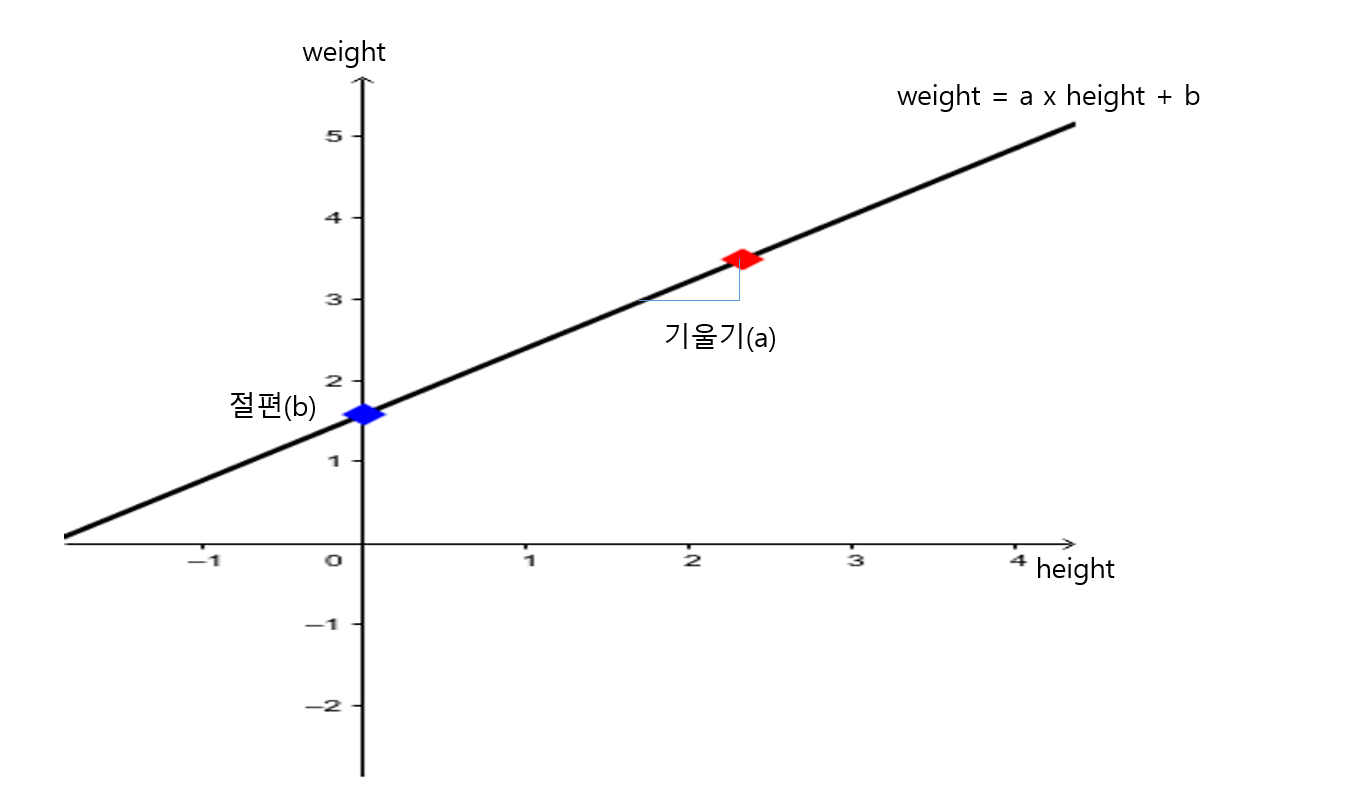
y = ax + b 우리가 옛날에 배웠던 직선의 방정식이다.
y = weight
x = height 라고 했을 때 
weight = a x height + b 가 된다.


이제 직선을 그리려면 기울기(a)와 절편(b)가 필요하다.
여기서 LinearRegression 클래스가 가장 잘맞는 기울기(a), 절편(b)를 찾아 준다. a,b 값은 coef_ 와 intercept_ 속성에 저장되어 있다.



직선 그려보기


height 10 부터 70 까지 직선을 그려보자. 아까 말한 coef_, intercept 각각 기울기, 절편을 사용하여 두 점을 이어주면 된다.

import matplotlib.pyplot as plt #그래프 그리는 패키지 import

plt.scatter(train_input, train_target, color='red')

#예측 데이터 그리기
plt.scatter([70], [1008.57662241], color='green', marker='*')

#직선 그리기
plt.plot([10, 70], [10*lr.coef_+lr.intercept_, 70*lr.coef_+lr.intercept_])

plt.xlabel('height')
plt.ylabel('weight')
plt.show()


그래프에 나와있는 직선이 선형 회귀 알고리즘이 데이터셋에서 찾은 최적의 직선이다.
선형 회귀 알고리즘을 사용하면 훈련세트에 벗어난 새로운 데이터도 충분히 예측이 가능해 진다.



전체 소스코드


import numpy as np

height = np.array([10.0,11.0,12.0,13.0,14.0,15.0,16.0,17.0,18.0,19.0,
                   20.5,21.0,22.0,23.0,24.0,25.0,26.0,27.5,28.0,29.0,
                   30.0,31.0,32.0,33.0,34.0,35.0,36.0,37.0,37.5,38.0,
                   39.0,40.0,41.0,42.0,43.0,44.0,45.0,46.0,47.0,48.0,
                   49.0,50.0,51.3,52.0,53.0,54.0,55.0,56.0,57.0,58.0
                    ])

weight = np.array([100.0,101.9,102.0,103.0,104.0,105.0,106.0,107.0,108.0,109.0,
                   110.0,110.0,111.0,120.0,121.0,122.0,124.0,126.0,127.0,128.0,
                   130.0,135.0,137.0,138.0,140.0,150.0,151.0,155.0,160.0,162.0,
                   170.0,180.0,190.0,200.0,300.0,400.0,500.0,600.0,700.0,800.0,
                   850.0,850.0,860.5,870.7,880.0,890.0,900.0,920.0,930.0,950.0
                    ])


#훈련세트,테스트 세트 나누기. random_stata를 42로 하면 프로그램을 껐다켜도 훈련세트와 테스트 세트의 샘플이 유지된다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
    height, weight, random_state=42)

# 2차원으로 바꾸기
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)

#모델 훈련 시키기
from sklearn.linear_model import LinearRegression

lr = LinearRegression()

#선형 회귀 모델 훈련
lr.fit(train_input, train_target)

# 예측하고 출력하기
print(lr.predict([[70]]))

import matplotlib.pyplot as plt #그래프 그리는 패키지 import

plt.scatter(train_input, train_target, color='red')

#예측 데이터 그리기
plt.scatter([70], [1008.57662241], color='green', marker='*')

#직선 그리기
plt.plot([10, 70], [10*lr.coef_+lr.intercept_, 70*lr.coef_+lr.intercept_])

plt.xlabel('height')
plt.ylabel('weight')
plt.show()



참조



혼자 공부하는 머신러닝 + 딥러닝(깃 허브) : https://github.com/rickiepark/hg-mldl

댓글

댓글 쓰기

이 블로그의 인기 게시물

[Python] 파이썬 if문 사용법과 예제

-
이미지
파이썬 if문 사용법과 예제 if문 이란? if문은 조건을 충족한다면 수행 하라는 조건문이다. 아래 그림처럼 조건문이 참이면 실행하고 거짓이면 다음 조건문으로 넘어간다. 사실 그림을 본다고 이해 안되므로 대충 보고 글을 차례대로 읽으면 이해가 될 것이다. if문의 기본 형태 아래 예제가 if문의 가장 간단한 형태로 if, else 두 개를 사용한다. if는 조건문으로 조건을 만족하면 실행한다. else는 조건을 만족하지 않으면 실행된다. 코드를 설명하자면 if 에서 점수(score)가 90점 이상이면 A등급을 출력한다. else 에서 90점 미만은 낙제를 출력한다. 첫 출부터 아래로 내려가면서 조건을 만족하면 실행한다. if 90<= score: 를 만났을 때 현재 score가 90이기 때문에 A등급을 출력 후 조건문이 종료 된다. 즉 else문은 실행되지 않는다. Tip) if문을 사용할 때 콜론( : )을 꼭 뒤에 붙여야 한다. 처음 하다 보면 콜론을 까먹는 경우가 있다.  score = 90 if 90 <= score: # '<=' 기호는 "같거나 크다." 로 사용된다. print ( "A 등급 " ) else : print ( " 낙제 " ) 결과 : A등급 elif 활용하기 바로 위에 예제는 하나의 조건 밖에 걸지 못한다. 하지만 elif를 사용한다면 여러 개의 조건을 걸 수 있다. 아래 예제를 보자. score는 현재 80점이다. 첫 줄 부터 코드가 진행된다. if 90<= score: 를 만났을 때 score는 90보다 작기 때문에 는 무시된다. if 80<= score: 를 만났을 때 score는 80과 같거나 크기 때문에 B등급이 출력된다. score = 80 if 90 <= score: print ( "A 등급 " ) el
다른 게시물 보기

[네트워크] 오류 제어 방식 이란?(FEC, BEC, ARQ)

-
오류 제어 방식 이란?(FEC, BEC, ARQ) 오류 제어 방식에 대해 알아보자.  통신에서 오류란? 송신한 데이터가 제대로 수신 측까지 가지 않았을 때 오류라고 한다. 오류의 원인에는 잡음(noise), 전송 기술, 채널 상태, 장비의 차이가 있다. 오류 제어 방식의 의미 데이터를 전송하는 과정에서 발생할 수 있는 오류를 감지하고 수정 또는 복구하는 방법. 오류 제어 방식의 종류 1. 오류 무시 2. 전진 오류 수정(FEC)     - 해밍 부호 검사 3. 후진 오류 수정(BEC)      - 패리티 검사     - 블록 합 검사     - 순환 중복 검사(CRC) 4. 검출 후 재전송(ARQ)      - 정지 대기(stop and wait) 방식      - go-back-N 방식      - selective-request 방식 5. 반항 검사 - 링크 계층에서 가장 많이 사용하는 오류제어 방식은 검출 후 재전송(ARQ) 다. - 반항 검사는 잘 사용하지 않으므로 다루지 않는다. 1. 오류 무시 - 오류 무시 정의 오류 무시란 오류가 발생한 프레임을 수신 측에서 버리거나 상위 계층에게 떠넘겨서 상위 계층에서 알아서 처리하게 하는 것. - 사용 예시 1. 100만큼 데이터를 보냈다고 했을 때, 20만큼 오류가 나더라도 상관 없을 때 사용. 2. 오류가 발생했던 데이터를 재전송 했을 때 시간이 지나 더 이상  수신 측에서 필요 없는 데이터일 때. 3. 음성 통신 같은 경우 내용 파악의 문제가 없으면 사용. 2. 전진 오류 수정(forward error correction) - 전진 오류 수정(FEC) 정의 전진 오류 수정이란 일정 한 비트 수 이하로 오류가 발생하면 수신 측에서 스스로 정정할 수 있도록 하는 것. 일정 한 비트 수의 의미는 오류가 100비트 발생하면 수정하기 힘들지만 한 두 개 정도는
다른 게시물 보기

[Virtual Box] 가상머신 에러 E_FAIL (0x80004005), (VERR_SUPLIB_PATH_NOT_CLEAN) 해결 방법

-
이미지
Failed to load R0 module D:\/VMMR0.r0: The path is not clean of leading double slashes: 'D:\/VMMR0.r0' (VERR_SUPLIB_PATH_NOT_CLEAN). E_FAIL (0x80004005) 인터페이스: IConsole {6ac83d89-6ee7-4e33-8ae6-b257b2e81be8} 해결 방법 에러 이유 ( VERR_SUPLIB_PATH_NOT_CLEAN) 결론 부터 말하자면 Virtual Box 경로가 C 드라이브가 아닌 D드라이브 같은 다른 위치에 설치되면 발생한다. VirtualboxVM.exe는 Virtualbox의 설치 폴더에 있어야 한다. virtualization support 설정, windows 보안 꺼도 에러가  해결 안되고 혹시 가상머신을 다른 경로에 저장했다면  이 방법을 써볼것. Vitual Box  재설치 후 경로 C드라이브로 설정 1. Vitual Box 제어판 가서 삭제한 후 재 설치한다. 2. 설치 하면서 가상 머신을 C드라이브로 설치한다. 괜히 D드라이브로 바꾸지 말 것.(그냥 경로 건들지 말자.) 에러 때문에 2시간 허비 했다. 에러 해결 방법에 대해 한국어 글이 없어서 누군가는 보라고 올림. 출처 :  https://forums.virtualbox.org/viewtopic.php?t=96445
다른 게시물 보기